| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- priority_queue
- Stack
- Visual Micro
- Array
- 라인트레이서
- 시스템프로그래밍
- 아두이노
- html
- c++
- Algorithm
- queue
- set
- LineTracer
- 수광 소자
- 운영체제
- 통계학
- 아두이노 컴파일러
- vector
- arduino compiler
- 아두이노 소스
- 컴퓨터 그래픽스
- Deque
- C언어
- WinAPI
- directx
- Arduino
- 자료구조
- list
- stl
- map
- Today
- Total
Kim's Programming
2차원 그래픽스의 변환 본문
2차원 그래픽스 변환
기본적인 기하변환
2차원 그래픽스 기하변환은 기본요소를 이동시키고, 크기를 바꾸고 회전을 시키는 등, 조작을 가해서 변형하거나 할 수 있습니다. 이러한 효과를 위해서 기하변환을 수행하며 기본적인 기하변환으로는 이동, 신축, 회전이 있습니다.
이동(Translation)
2차원 평면에서 객체의 이동변환은 모양은 변하지 않고 객체의 치를 일정한 거리만큼 다른 위치로 옮기는 변환입니다. x 방향으로 tx, y방향으로 ty만큼으로 이동한 점의 식은 다음과 같이 하게됩니다.
위의 식들을 행렬을 이용하여 표현하게 되면 다음과 같이 나타나게 됩니다.
신축(Scale)
2차원 평면에서 신축변환은 x방향 및 y방향으로 확대 또는 축소시키는 기하변환입니다. 신축변환의 경우는 일반적으로 원점을 기준으로 신축을 하게됩니다. 평면상에서 임의의 점을 x 방향으로 Sx배, y방향으로 Sy배 만큼의 신축배율을 적용하여 변환하는 식은 다음과 같습니다.
위의 식들을 행렬을 이용하여 표현하게 되면 다음과 같이 나타나게 됩니다.
원점이 아닌 임의의 점(x0,y0)를 기준으로 회전을 시키는 것은 다음과 같이 과정을 거치게 됩니다.
: 신축 기준점이 원점과 일치하도록
만큼 이동시킵니다.
: 이동변환된 객체 b를 원점을 기준으로 하여
배 만큼 신축변환을 합니다.
: 신축된 객체를 다시 원래 기준점 위치로 이동시키면 신축결과를 얻을 수 있습니다.
임의의점 (x0,y0)을 원점으로 이동한뒤 다시 원래대로 옮겨줍니다. 위의 과정을 하는 식은 다음과 같이 됩니다.
회전(Scale)
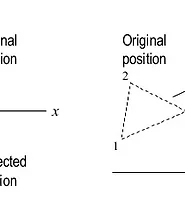
2차원 평면에서 객체를 회전시키면 모양의 변화는 없이 객체가 놓여 있는 방향이 변하게됩니다. 회전변환도 신축변화과 같이 기준점이 필요하며 기준점을 중심으로 회전하게 됩니다. 회전각이 양수이면 반시계 음수이면 시계방향으로 회전합니다. x축과 기존의 도형이 이루는 각도를 '파이' 위 그림에서 알파에 해당하는 것을 세타라고 하고 점과 원점 사이의 거리를 r이라고 봤을 때 다음과 같이 정리 할 수 있습니다.
다음의 경우를 행렬로 나타나게 되면 다음과 같이 나타낼 수 있습니다.
신축과 같이 중심점이 원점이 아니라 임의의 점 (x0,y0)인 경우도 역시 신축과 같이 다음과 같이 되게 됩니다.
: 신축 기준점이 원점과 일치하도록
만큼 이동시킵니다.
: 이동변환된 객체 b를 원점을 기준으로
도 만큼 회전변환을 합니다.
: 신축된 객체를 다시 원래 기준점 위치로 이동시키면 신축결과를 얻을 수 있습니다.
'Computer Theory > Computer Graphics' 카테고리의 다른 글
| 래스터 변환과 2차원 윈도우 (0) | 2016.01.24 |
|---|---|
| 2차원 그래픽스의 동차좌표계 변환 (0) | 2016.01.23 |
| 2차원 그래픽스 문자와 색상 표현 (0) | 2016.01.23 |
| 2차원 그래픽스 다각형 영역과 채우기 (0) | 2016.01.23 |
| 2차원 그래픽스 기본요소와 그리기(2/2) (0) | 2016.01.23 |