Notice
Recent Posts
Recent Comments
| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
Tags
- 아두이노 소스
- C언어
- 자료구조
- arduino compiler
- c++
- map
- set
- vector
- directx
- queue
- 수광 소자
- 운영체제
- Stack
- WinAPI
- 컴퓨터 그래픽스
- stl
- 시스템프로그래밍
- LineTracer
- 통계학
- Deque
- list
- Array
- priority_queue
- 아두이노
- Arduino
- html
- 라인트레이서
- Algorithm
- Visual Micro
- 아두이노 컴파일러
Archives
- Today
- Total
Kim's Programming
[C로 만드는 자료구조]우선순위 큐(Priority Queue) 본문
우선순위 큐(Priority Queue) - 정의
우선순위 큐란 우선 순위를 가진 항목들을 저장하는 큐 입니다. 즉, 우선 순위가 높은 데이터가 먼저 나갑니다.
우선순위 큐(Priority Queue) - 활용
우선순위 큐의 활용 분야는 다음과 같습니다.
- 시뮬레이션 시스템 (사건의 시각 입장으로)
- 네트워크 트래픽 제어
- OS 작업 스케줄링
우선순위 큐(Priority Queue) - 다른 자료구조와의 차이
자료구조 |
삭제되는 요소 |
스택(Stack) |
가장 최근에 들어온 데이터 |
큐(Queue) |
가장 먼저 들어온 데이터 |
유선순위 큐(priority Queue) |
가장 우선순위가 높은 데이터 |
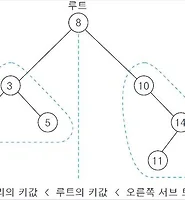
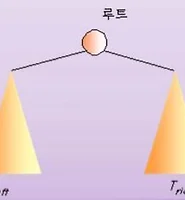
우선순위 큐(Priority Queue) - 힙(Heap)으로 구현
우선순위 큐의 구현은 힙(Heap)을 이용합니다. 힙이란 완전 이진 트리에 있는 노드 중에서 키 값이 가장 큰 노드나 키 값이 가장 작은 노드를 찾기 위해서 만든 자료구조입니다.
- 최대 힙 (Max Heap)
- 키 값이 가장 큰 노드를 찾기 위한 완전 이진 트리
- 루트 노드 : 키 값이 가장 큰 노드
- 부모 노드의 키 값 >= 자식 노드의 키 값
- 최소 힙(Min Heap)
- 키 값이 가장 작은 노드를 찾기 위한 완전 이진 트리
- 루트 노드 : 키 값이 가장 작은 노드
- 부모노드의 키 값 <= 자식 노드의 키 값
최대 힙과 최소 힙의 형태는 다음과 같습니다.
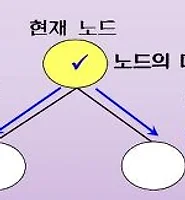
우선순위 큐(Priority Queue) - 힙(Heap)으로 구현 - 구현 (삽입)
힙(heap)에서의 삽입 연산은 다음과 같은 원칙을 따릅니다.
- 완전 이진 트리를 유지하면서, 확장한 노드에 삽입할 원소 저장
- 노드가 n개인 완전 이진 트리에서 다음 노드의 확장 자리는 n+1번의 노드가 된다.
- n+1번 자리에 노드를 확장하고, 그 자리에 삽입할 원소를 저장한다.
- 만들어진 완전 이진 트리 내에서 삽입 원소의 제자리를 찾기
- 현재 위치에서 부모 노드와 비교하여 크기 관계를 확인한다.
- 현재 부모 노드의 키 값 >= 삽입원소의 키 값(최대 힙 기준)의 관계가 성립하지 않으면 현재 부모노드의 원소와 삽입 원소의 삽입 원소의 자리를 서로 바꾼다.
힙의 삽입 알고리즘은 다음과 같이 그림으로 나타내지게 됩니다.
우선순위 큐(Priority Queue) - 힙(Heap)으로 구현 - 구현 (삭제)
힙(heap)에서의 삭제는 다음의 규칙을 따릅니다.
우선 삭제는 루트 노드의 원소만 삭제할 수 있습니다.
- 루트 노드의 원소를 삭제하여 반환한다.
- 원소의 개수가 n-1개로 줄었으므로, 노드의 수가 n-1인 완전 이진 트리로 조정한다.
- 노드가 n개인 완전 이진 트리에서 노드 수 n-1개의 완전 이진 트리가 되기 위해서 마지막 노드, 즉 n번 노드를 삭제
- 삭제된 n번 노드에 있던 원소는 비어있는 루트 오드에 저장
- 완전 이진 트리 내에서 루트에 임시 저장된 원소의 제자리를 찾아가도록 한다
- 현재 위치에서 자식 노드와 비교하여 크기 관계를 확인
- 현재 위치의 키 값 >= 현재 자식 노드의 키 값(최대힙 기준)의 관계가 성립하지 않으면 ,현재 자식 노드의 원소와 현재 위치에 저장된 원소의 자리를 서로 바꾼다.
힙에서의 삭제를 그림으로 나타내면 다음과 같이 표현됩니다.
우선순위 큐(Priority Queue) - 힙(Heap)으로 구현- ADT
우선순위 큐를 구현할 때는 다음의 구조체들을 이용해서 만들게 됩니다.
1 2 3 4 5 6 7 8 9 10 11 12 | #include<stdio.h> #define MAX_SIZE 15 struct TreeNode { int data; }; struct Tree { int cur = 1; TreeNode Array[MAX_SIZE]; }; | cs |
- Add_Tree()123456789101112131415161718192021222324252627int Compare_Add(Tree *Target_Tree, int Position)//삽입후 비교{int temp;if (Target_Tree->Array[Position].data < Target_Tree->Array[Position / 2].data || Position == 1)//부모가 더큼return 0;if (Target_Tree->Array[Position].data > Target_Tree->Array[Position/2].data)//부모가 작음{temp = Target_Tree->Array[Position].data;Target_Tree->Array[Position].data = Target_Tree->Array[Position / 2].data;Target_Tree->Array[Position / 2].data = temp;return Compare_Add(Target_Tree,Position/2);}return 0;}void Add_Tree(Tree *Target_Tree, int Item)//삽입{if (Target_Tree->cur == 1){Target_Tree->Array[Target_Tree->cur].data = Item;Target_Tree->cur += 1;return;}Target_Tree->Array[Target_Tree->cur].data = Item;Compare_Add(Target_Tree, Target_Tree->cur);Target_Tree->cur += 1;}
cs 데이터를 삽입하는 함수입니다. 단일 함수로 만들기가 힘들어서 단순삽입용 함수와 자리 잡는 함수 두개로 나누어 구현했습니다.
Delete_Root()
12345678910111213141516171819202122232425262728293031323334353637int Compare_Delete(Tree *Target_Tree, int Position){if (Position > Target_Tree->cur){return 0;}int next = 0;int temp;if (Target_Tree->Array[Position * 2].data > Target_Tree->Array[Position * 2 + 1].data)if (Target_Tree->Array[Position + 2].data < Target_Tree->Array[Position].data)return 0;elsenext = 0;//왼쪽이 더 큼을 판단elseif (Target_Tree->Array[Position + 2 + 1].data < Target_Tree->Array[Position].data)return 0;elsenext = 1;//오른쪽이 더 큼을 판단temp = Target_Tree->Array[Position * 2 + next].data;Target_Tree->Array[Position * 2 + next].data = Target_Tree->Array[Position].data;Target_Tree->Array[Position].data = temp;return Compare_Delete(Target_Tree, Position * 2 + next);//다음 위치로 이동하여 재판단}int Delete_Root(Tree *Target_Tree){int temp;if (Target_Tree->cur == 1){Target_Tree->cur -= 1;return Target_Tree->Array[Target_Tree->cur+1].data;}temp = Target_Tree->Array[1].data;Target_Tree->Array[1].data = Target_Tree->Array[Target_Tree->cur].data;Compare_Delete(Target_Tree, 1);Target_Tree->cur -= 1;return 0;}cs 삭제를 하기위해 루트를 삭제하는 함수입니다. 이 또한 비교과정과 단순 삭제부분을 나눠서 구현했습니다.
다음 포스팅에서는 이진 탐색 트리에 대해서 포스팅하겠습니다.
'Programming > Data Structure' 카테고리의 다른 글
| [C++/템플릿으로 만드는 자료구조] 단순연결리스트(Linked List) (1) | 2016.01.18 |
|---|---|
| [C로 만드는 자료구조]이진 탐색 트리(Binary Search Tree) (16) | 2015.12.25 |
| [C로 만드는 자료구조]이진 트리(Binary Tree) - 순회 (0) | 2015.12.18 |
| [C로 만드는 자료구조]이진 트리(Binary Tree) - 배열 (6) | 2015.12.17 |
| [C로 만드는 자료구조]트리(Tree) (0) | 2015.12.16 |