| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
- stl
- Algorithm
- WinAPI
- C언어
- priority_queue
- map
- vector
- arduino compiler
- 라인트레이서
- 자료구조
- 컴퓨터 그래픽스
- 수광 소자
- set
- queue
- Array
- list
- Deque
- 통계학
- directx
- html
- c++
- Stack
- 운영체제
- LineTracer
- 아두이노 소스
- 시스템프로그래밍
- 아두이노
- 아두이노 컴파일러
- Arduino
- Visual Micro
- Today
- Total
Kim's Programming
3차원 그래픽스 투영을 위한 변환 본문
투영을 위한 변환
뷰볼륨(View Volume)
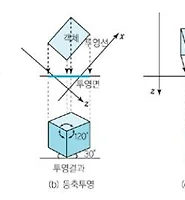
튜영변환에서 뷰 평면의 윈도우에 튜영되는 객체들은 3차원 공간에서 일정한 영역을 뷰 볼륨이라고 하며 투영방법에 따라서 뷰볼륨의 모양도 달라집니다. 위에 있는 그림의 경우는 원근투영의 경우이며 뷰 볼륨의 모양이 윗부분이 절단된 사각뿔의 형태인 프러스텀 뷰볼륨(Frustum View Volume)이라고 하며 평행투행에서는 뷰볼륨의 모양이 직육면체의 형태를 가지게 때문에 평행뷰 볼륨이라고 부릅니다.
평행투영(Parallel Projection)의 변환행렬
1) 직각투영(Orthographic Projection)
직각투영의 경우 뷰볼륨이 직육면체 형태이며 뷰잉 좌표계의 각 축에 수직방향으로 놓여있습니다. 따라서 축의 방향으로 직각 투영을 하면 앞에서 보았듯이 그 축에 해당하는 좌표 값만 0으로 바꾸면 되게 됩니다. 각각 x축, y축, z축 방향으로 투영하는 식입니다.
2) 경사투영(Oblique Projection)
경사투영은 경사투영을 평행투영으로 밀림변환을 한 다음 평행투영을 하게 됩니다.
점 P를 직각 투영한 점 (x,y,0)과 경사 투영한점 P'사이의 선분 길이를 L, 이 선분이 x축과 이루는 각도는 파이라고 하면 좌표값은 다음과 같이 구할 수 있습니다.
평행투영(Parallel Projection)의 변환행렬
계산상의 편의를 위해 시점을 뷰잉좌표계의 원점에 위치시키고, 윈도우가 설정되는 뷰평면의 법선벡터를 z축 방향이라고 하겠습니다. 뒷 평면과 앞 평면의 z좌표인 -F와 -N의 값이 필요하고 윈도우가 있는 뷰평면의 z좌표 위치인 -d의 값이 필요합니다. 또 윈도우에서 왼쪽 경계인 최소 x값을 L. 아래 최소 y좌표값을 B, 오른쪽 경계 최대 x좌표값을 R 위쪽 최대 y좌표값을 T라 할때 이들 좌표값을 지정하면 프러스텀 뷰 볼륨의 모양이 결정됩니다.
뷰볼륨 내의 P(x,y,z)가 뷰 평면 z = -d에 원근 투영이 된 점 Q(Xp,Yp)는 다음의 3단계 과정으로 구할 수 있습니다.
- 밀림 변환
: 경사원근투영의 뷰볼륨을 직각원근 투영의 뷰 볼륨으로 변환합니다. 경사 원근투영에서의 점 P(x,y,z)를 직각원근투영으로 변환시킨 점 P'(x',y',z')을 구합니다.
- 신축변환
: 직각원근투영의 뷰 볼륨을 45도 각도의 뷰볼륨으로 신축변환을 합니다. 이전 단계에서 구한 점 P'(x',y',z')을 기하변환시킨 점 P''(x'',y'',z'')를 구합니다.
- 정규화
: 직각원근투영의 뷰볼륨을 정육면체 형태로 정규화하여 직각투영이 적용되도록 만듭니다. 앞 단계에서 구한 점 P''(x'',y'',z'')를 구하고 이를 직각투영시켜 투영점 Q(xp,yp)를 구합니다.
직각투영을 이용하여 원근투영된 점을 구하는 과정에 대한 식을 합성해서 만들면 다음과 같이 나다낼 수 있습니다.
'Computer Theory > Computer Graphics' 카테고리의 다른 글
| 3차원 그래픽스 객체의 모델링(2/2) (0) | 2016.01.25 |
|---|---|
| 3차원 그래픽스 객체의 모델링(1/2) (0) | 2016.01.25 |
| 3차원 그래픽스 투영의 종류 (0) | 2016.01.24 |
| 3차원 그래픽스 기하변환 (4) | 2016.01.24 |
| 3차원 그래픽스 (0) | 2016.01.24 |