| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 아두이노 소스
- Deque
- vector
- 자료구조
- c++
- html
- Array
- list
- queue
- 아두이노
- C언어
- stl
- map
- Visual Micro
- 컴퓨터 그래픽스
- 라인트레이서
- directx
- WinAPI
- 수광 소자
- Algorithm
- priority_queue
- set
- Arduino
- 운영체제
- arduino compiler
- Stack
- 통계학
- 아두이노 컴파일러
- 시스템프로그래밍
- LineTracer
- Today
- Total
목록전체 글 (545)
Kim's Programming
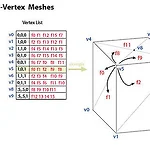 3차원 그래픽스 객체의 모델링(1/2)
3차원 그래픽스 객체의 모델링(1/2)
3차원 모델링 3차원 객체 모델링 단각형 매쉬(Polygon Mesh) : 여러가지 크기와 모양의 다각형들이 그물 모양으로 연결 된 것 곡면 모델링 : 부드러운 곡면을 표현하기 위하여 항상 이러한 수학함수를 적용할 수 있는 것은 아니지만 자동차나 비행기의 표면과 같은 부드러운 곡면을 설계할떄 이용 스위핑(Sweeping) : 원을 밀어서 원기둥, 원을 회전 시켜 도넛형태등으로 만듬 솔리드 모델링(Solid Modeling) : 육면체, 구, 원기둥과 같은 객체를 결합하거나 조합하여 만듬 절차적 함수 : 자연물, 장연현상을 나타내기 위해 프렉탈 기하학이나 입자시스템을 적용 1) 다각형 매쉬(Polygon Mesh) 모양과 연결하는 방법에 따라 3차원 객체를 근사적으로 표현할 수 있습니다. 삼각형을 이용하여..
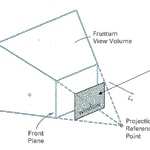 3차원 그래픽스 투영을 위한 변환
3차원 그래픽스 투영을 위한 변환
투영을 위한 변환 뷰볼륨(View Volume) 튜영변환에서 뷰 평면의 윈도우에 튜영되는 객체들은 3차원 공간에서 일정한 영역을 뷰 볼륨이라고 하며 투영방법에 따라서 뷰볼륨의 모양도 달라집니다. 위에 있는 그림의 경우는 원근투영의 경우이며 뷰 볼륨의 모양이 윗부분이 절단된 사각뿔의 형태인 프러스텀 뷰볼륨(Frustum View Volume)이라고 하며 평행투행에서는 뷰볼륨의 모양이 직육면체의 형태를 가지게 때문에 평행뷰 볼륨이라고 부릅니다. 평행투영(Parallel Projection)의 변환행렬 1) 직각투영(Orthographic Projection) 직각투영의 경우 뷰볼륨이 직육면체 형태이며 뷰잉 좌표계의 각 축에 수직방향으로 놓여있습니다. 따라서 축의 방향으로 직각 투영을 하면 앞에서 보았듯이 그..
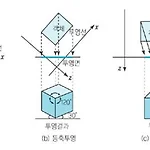 3차원 그래픽스 투영의 종류
3차원 그래픽스 투영의 종류
투영의 종류 투영방식은 상대적인 크기가 유지되는 평행투영(Parallel Projection)과 거리에 따라 크기가 다르게 투영되는 원근투영(Perspective Projection)으로 구분됩니다. 평행투영(Parallel Projection) 평행투영에서는 3차원 객체를 2차원 평면인 투영면에 일정한 각도로 투영을 시키며, 이 경우 모든 투영선이 평행이므로 원래 객체들 간의 상대적인 크기가 그대로 유지됩니다. 평행투영은 직각투영, 등축투영, 경사투영으로 분류됩니다. 1) 직각 투영(Orthographic Projection) 직각 투영은 3차원 공간의 좌표계에서 x, y, z축 가운데 한 축과 투영방향이 동일하고 투영면은 이 축과 직각이 되도록 배치하여 투영하는 방법을 의미합니다. 직각투영은 처리과정..
 3차원 그래픽스 기하변환
3차원 그래픽스 기하변환
3차원 기하변환 이동(Translation) 3차원 공간에서 객체의 이동은 2차원 객체와 마찬가지로 다면체를 구성하는 각 꼭지점을 이동시키고 난다음 이들을 연결하여 다면체를 새로 그리면 됩니다. 3차원 공간에서의 한점 P(x,y,z)가 각 축 방향으로 (tx,ty,tz)만큼 이동한점 P'(x',y',z')의 좌표는 다음과 같이 나타냅니다. 또한 동차좌표계를 이용한 행렬로 표현하면 다음과 같이 됩니다. 신축(Scale) 3차원 공간에서 P(x,y,z)를 원점을 기준으로 하여 각 축의 방향으로 (sx,sy,sz)배 만큼 신축변환을 수행한 점 P'(x',y',z')를 다음과 같이 표현이 가능하며 또한 동차좌표계를 이용한 행렬로 표현하면 다음과 같이 됩니다. 만약 원점이 기준이 아니라 (x0, y0, z0) 기..
 3차원 그래픽스
3차원 그래픽스
3차원 그래픽스 3차원 그래픽스의 처리과정 3차원 객체 또한 모델링(Modeling), 투영(Projection), 렌더링(Rendering) 과정을 거치게 됩니다. 1) 모델링(Modeling) 3차원 그래픽스에서는 모델링 방법이 2차원과는 조금 다릅니다. 다음 5가지 방법을 이용합니다. 다각형 표면 모델링(Polygon Surface Modeling) 매개변수 이용 곡면 모델링(Paramectric Surface Modeling) 솔리드 모델링(Solid Modeling) 스위핑(Sweeping) 프렉탈(Fractal 기하학이나 입자 시스템) 2) 투영(Projection) 3차원 그래픽스에서 모니터가 2차원 평면이기 때문에 투영하는 과정이 필요합니다. 투영과정은 원근투영, 평행투영 2가지가 있습니다..
 래스터 변환과 2차원 윈도우
래스터 변환과 2차원 윈도우
래스터 방식 변환 래스터 변환 래스터 방식에서 객체의 변환을 할 때는 프레임버퍼 내의 사각형 모양에 해당하는 픽셀블록을 조작합니다. 픽셀블록들에 대해서 덧셉 곱셈같은 연산이 아니라 AND, OR 등 비트연산을 사용하여 픽셀블록들을 조작하여 변환시킵니다. 이러한 변환을 처리하는 래스터 함수들을 래스터연산 또는 RasterOp 라고 부릅니다. 또한 래스터 변환은 다른 위치로 옮기며 처리하는 과정이므로 bitBlt(Bit Block Transfer)라고도 불립니다. 래스터 변환 래스터 방식으로 표현된 객체 또는 프레임 버퍼내의 픽셀블록을 조작하여 변환하는 래스터연산(RasterOp)에서는 주로 COPY, OR, XOR, AND, ERASE, SET, CLEAR등의 비트 연산이 사용됩니다. 글자영역을 S, 커서..
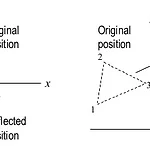 2차원 그래픽스의 동차좌표계 변환
2차원 그래픽스의 동차좌표계 변환
동차좌표계 변환 동차좌표계를 써야 하는 이유 앞에서 봤던 변환에서 이동은 더하기 연산이며 신축변환과 회전 변환은 곱셈을 하는 변환입니다. 하지만 곱셈과 덧셈이 많아지기 때문에 계산량이 크게 증가하게 됩니다. 하지만 단순하게 곱하기만 연속해서 하게 된다면 계산이 간단해 지게 됩니다. 그렇게 하기 위하여 동차좌표계를 쓰게 됩니다. 동차좌표계의 표현 2차원의 평면에서 한 점 P(x,y)를 동차좌표계로 표현하면 차원이 하나 증가되어 임의의 h!=0에 대하여 P(hx,hy,h)의 형태로 표현하게됩니다. 만약 동차 좌표계에서 h=1인 경우에는 점 P(x,y,1)이 그대로 2차원 좌표 P(x,y)로 대응되므로 별도의 나눗셈이나 곱셈을 할 필요가 없습니다. 따라서 일반적으로 계산의 편의를 위하여 평면상의 점 P(x,y..
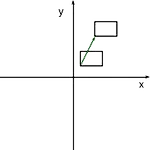 2차원 그래픽스의 변환
2차원 그래픽스의 변환
2차원 그래픽스 변환 기본적인 기하변환 2차원 그래픽스 기하변환은 기본요소를 이동시키고, 크기를 바꾸고 회전을 시키는 등, 조작을 가해서 변형하거나 할 수 있습니다. 이러한 효과를 위해서 기하변환을 수행하며 기본적인 기하변환으로는 이동, 신축, 회전이 있습니다. 이동(Translation) 2차원 평면에서 객체의 이동변환은 모양은 변하지 않고 객체의 치를 일정한 거리만큼 다른 위치로 옮기는 변환입니다. x 방향으로 tx, y방향으로 ty만큼으로 이동한 점의 식은 다음과 같이 하게됩니다. 위의 식들을 행렬을 이용하여 표현하게 되면 다음과 같이 나타나게 됩니다. 신축(Scale) 2차원 평면에서 신축변환은 x방향 및 y방향으로 확대 또는 축소시키는 기하변환입니다. 신축변환의 경우는 일반적으로 원점을 기준으로..
